​

Saturday, July 10, 2021

Gravity Part 3: Create a force map and display it (CPU, Compute Shader and Fragment Shader)

Introduction

This is the third and last post in the series I am creating, based on the logic from Physics-based Solar System Lessons:
The interesting thing about this post is that there is no intrinsic changes to the physics or calculations. This is just a way to visualize forces in texture.

Gravity Part 3: Create a force map and display it

In Gravity Part 1 I polished a system that creates movement out of objects due to their gravitational force. Wouldn't it be interesting to visualize these forces somehow? This is not difficult but has a very big problem: these calculations need to be reevaluated every frame and then painted to a texture.

Artistic color representation for force direction by Shutterstock


To visualize this, I created 3 independent systems that calculate the gravity forces and then paint the texture:
  • CPU: CPU calculation, CPU painting.
  • Compute Shader: Compute Shader calculation, CPU painting.
  • Fragment Shader: Fragment Shader calculation, Fragment Shader painting.
For each case I will show calculations, source code and results. At the end I will compare all three cases and give a conclusion.
 

Initial Setup

First we need to create a Plane with the dimensions we want it to cover, and then attach the desired script to be used. The beautiful thing about the current approach is that the initial setup is almost the same for each case of texture painting.
  • CPU: enable script. Material set to Unlit/Texture.
  • Compute shader: enable script. Material set to Unlit/Texture.
  • Fragment Shader: enable script. Material set to Gravity/ForceMap.
For easier visualization check the following screenshots:

Setup for CPU/Compute Shader scripts and texture

Setup for Fragment Shader script and texture


General remarks
Force representation: In the texture we will be using a clamped logarithm scale. Following Newton’s gravity force equation produces an exponential function, which means there will be a lot of near-zero values that will not be properly displayed (but are relevant).

\[F = G\dfrac{m_1 m_2}{r^2}\]  

If we just use these values to paint, we will mostly see a bright color area around large gravity sources and everything else will be mostly blackish. By using a logarithm scale, we can see more clearly the dominant force direction in each point. If the color is close to black, then there is virtually no net force (specially in a Log scale).

Log(x) by WolframAlpha

Color representation: I will be using an RGB color representation to visualize 4 force directions (we are painting on a 2D plane, so we will ignore anything from the third axis):
  • Red: Force towards “left” of texture.
  • Green: Force towards “right” of texture.
  • Blue: Force towards “top” of texture.
  • Yellow: Force towards “bottom” of texture.
Below is the Force map texture legend:


Directions of forces are represented by  colors

Black means neutral direction of force.

CPU

This is the simplest approach; I directly use the logic I had already created in previous posts. For simplicity I redesigned all the logic within the same script, so everything is just in one place. The logic is:
  1. Initialization:
    1. Setup texture size and properties.
    2. Create world points for the texture.
  2. Update texture:
    1. Calculate forces: For each texture pixel get the net force.
    2. Paint forces: For each net force paint in the texture with a certain color
    3. Update texture from painted pixels.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
using System;
using System.Linq;
using UnityEngine;

public class ForceMapCpu : MonoBehaviour
{
    [Header("Texture details")]
    [SerializeField] private Vector2 _textureResolution = new Vector2(1000, 1000);
    [Tooltip("Regardless of texture Y position, do the calculations as if Y = value")]
    [SerializeField] private float _positionTextureY = 0; 

    private Texture2D _texture;
    private Color[] _texturePixelsColor; //All the points in the texture with a set color in each pixel
    private Vector3[] _texturePixelPositions; //Each Pixel in the texture is mapped to a world coordinate

    private float _maxForce; //Used to clamp the force visualization
    private SpaceObject[] _spaceObjects;

    private float _time;
    private float _waitSeconds = 0.01f;

    void Start()
    {
        _time = Time.realtimeSinceStartup;

        var spaceObjects = GameObject.FindGameObjectsWithTag("SpaceObject").Where(o => o.gameObject != gameObject).ToList();
        _spaceObjects = spaceObjects.Select(p => p.GetComponent<SpaceObject>()).ToArray();
        _maxForce = GetMaximumGravity();

        _texture = new Texture2D((int)_textureResolution.x, (int)_textureResolution.y)
        {
            wrapMode = TextureWrapMode.Clamp,
            filterMode = FilterMode.Bilinear
        };

        GetComponent<Renderer>().material.mainTexture = _texture;
        
        _texturePixelsColor = new Color[_texture.height * _texture.width];
        _texturePixelPositions = GetTextureWorldPoints();
    }

    void Update()
    {
        if (_time + _waitSeconds <= Time.realtimeSinceStartup)
        {
            PaintForceMap();

            _time = Time.realtimeSinceStartup;
        }
    }

    private float GetMaximumGravity()
    {
        var maxForce = float.MinValue;

        foreach (var spaceObject in _spaceObjects)
        {
            var force = GetGravity(spaceObject, spaceObject.transform.position + new Vector3(1.0f, 1.0f, 1.0f));

            if (maxForce <= force.magnitude)
            {
                maxForce = force.magnitude;
            }
        }

        return maxForce;
    }

    // Apply Log to the gravity to ease visualization of the force
    private Vector3 GetGravity(SpaceObject spaceObject, Vector3 atPoint)
    {
        var direction = spaceObject.transform.position - atPoint;
        var gravityLog = Math.Log(1 + spaceObject.GetGravitationalPullForce(direction.magnitude));

        return direction.normalized * (float)gravityLog;
    }


    private Vector3[] GetTextureWorldPoints()
    {
        var worldPoints = new Vector3[_texture.height * _texture.width];

        for (int i = 0; i < _texture.height; i++)
        {
            for (int j = 0; j < _texture.width; j++)
            {
                var localPoint = TransformTextureCoordinateToLocalCoordinates(i, j, _texture);
                var worldPoint = transform.TransformPoint(localPoint);
                worldPoint.y = _positionTextureY; //We want to check with respect to reference planet (usually Earth) and not actual position of texture
                worldPoints[j * _texture.height + i] = worldPoint;
            }
        }

        return worldPoints;
    }

    // From i,j position in texture to a local Vector3
    private Vector3 TransformTextureCoordinateToLocalCoordinates(int i, int j, Texture2D texture)
    {
        var posX = 5 - 10 * (i + 0.5f) / texture.height;
        var posZ = 5 - 10 * (j + 0.5f) / texture.width;

        return new Vector3(posX, 0, posZ);
    }

    private void PaintForceMap()
    {
        for (int i = 0; i < _texture.height; i++)
        {
            for (int j = 0; j < _texture.width; j++)
            {
                var clampedForce = GetGravityAtPoint(_texturePixelPositions[j * _texture.height + i]) / _maxForce;
                var color = GetColorFromForce(clampedForce);

                _texturePixelsColor[j * _texture.height + i] = color;
            }
        }

        _texture.SetPixels(_texturePixelsColor);
        _texture.Apply();
    }

    private Vector3 GetGravityAtPoint(Vector3 point)
    {
        var netForce = new Vector3();

        foreach (var spaceObject in _spaceObjects)
        {
            var force = GetGravity(spaceObject, point);
            netForce += force;
        }

        return netForce;
    }

    private Color GetColorFromForce(Vector3 force)
    {
        var colorForce = Color.black;

        if (force.z > 0.0f && force.x > 0.0f)
        {
            colorForce.b = force.z;
            colorForce.g = force.x;
        }
        else if (force.z > 0.0f && force.x <= 0.0f)
        {
            colorForce.b = force.z;
            colorForce.r = -force.x;
        }
        else if (force.z <= 0.0f && force.x > 0.0f)
        {
            colorForce.r = -force.z;
            colorForce.g = Mathf.Sqrt(Mathf.Pow(force.z, 2) + Mathf.Pow(force.x, 2));
        }
        else if (force.z <= 0.0f && force.x <= 0.0f)
        {
            colorForce.r = Mathf.Sqrt(Mathf.Pow(force.z, 2) + Mathf.Pow(force.x, 2));
            colorForce.g = -force.z;
        }

        return colorForce;
    }
}


How to paint pixels in a texture. Technically there are two easy ways to change pixels in a texture in Unity [1]:
  • SetPixel: only sets 1 pixel at a time.
  • SetPixels: set a whole block of pixels. I used this as it is more efficient in our case.

Optimization

When I first created this script I used small texture sizes, and still got decent framerates (60+ FPS), as I increased the texture size the FPS reduced drastically. One way to optimize it is not to calculate in every update call, but whenever is necessary. That is why I am using a time delay to paint the force map.

Compute Shader

The logic here is a bit more complex. We have 2 scripts:
  • CSForceMap.compute: This is a file that uses shader language and will be ran in the GPU.
  • ForceMapComputeShader.cs: This script loads the information into the GPU, retrieves it and then paints it.
The compute shader has all the logic to calculate the gravity source per location. The key here is to update the gravity sources when needed (usually during an Update) and do every pixel calculation in the GPU. For this there are a few variables that depend on outside parameters. I use arrays that can be Read/Write capability from inside/outside the GPU (RWStructuredBuffer<type>). As a reference I used Unity official’s documentation [2], Ronja’s tutorials [3] and Nvidia’s reference [6].

CSForceMap.compute 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#pragma kernel CSForceMap

struct Source
{
    float3 position;
    float mu;
};

//Constants. Set in initialization
uint sizeX;
uint sizeY;
uint numSources;
float maxForce;
RWStructuredBuffer<float3> pixelPositions;

//Dynamic variables
RWStructuredBuffer<Source> gravSources; //This gets updated asyncronously 
RWStructuredBuffer<float4> forcesInColor; //Contains the data to be retrieved from the C# script

float4 GetColorFromGravity(float3 force)
{
    float4 colorForce = float4(0, 0, 0, 0);

    if (force.z > 0.0f && force.x > 0.0f)
    {
        colorForce.b = force.z;
        colorForce.g = force.x;
    }
    else if (force.z > 0.0f && force.x <= 0.0f)
    {
        colorForce.b = force.z;
        colorForce.r = -force.x;
    }
    else if (force.z <= 0.0f && force.x > 0.0f)
    {
        colorForce.r = -force.z;
        colorForce.g = sqrt(pow(force.z, 2) + pow(force.x, 2));
    }
    else if (force.z <= 0.0f && force.x <= 0.0f)
    {
        colorForce.r = sqrt(pow(force.z, 2) + pow(force.x, 2));
        colorForce.g = -force.z;
    }

    return colorForce;
}

[numthreads(32, 1, 1)]
void CSForceMap(uint3 id : SV_DispatchThreadID)
{
    float3 netForce = float3(0, 0, 0);

    for (uint k = 0; k < numSources; ++k)
    {
        float3 forceDirection = (gravSources[k].position - pixelPositions[id.x]);
        float gravityLog = log(1 + gravSources[k].mu / dot(forceDirection, forceDirection));
        netForce += normalize(forceDirection) * gravityLog;
    }

    forcesInColor[id.x] = GetColorFromGravity((netForce / maxForce));
}


The other piece of code has a very similar logic to the previous implementation using only CPU:
  1. Initialization:
    1. Setup texture size and properties.
    2. Create world points for the texture.
    3. Initialize Compute Shader variables: We need to set the dynamic variables before executing the compute shader.
  2. Update Compute Shader variables:
    1. Send updated gravity sources to GPU.
    2. Compute shader doing magic: Note that this is happening in parallel to this list.
    3. Retrieve texture pixel values (gravity forces are now colors)
    4. Update texture from retrieved pixels.
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
using System;
using System.Linq;
using UnityEngine;

public class ForceMapComputeShader : MonoBehaviour
{
    [Header("Texture details")]
    [SerializeField] private Vector2 _textureResolution = new Vector2(512, 512);
    [Tooltip("Regardless of texture Y position, do the calculations as if Y = value")]
    [SerializeField] private float _positionTextureY = 0;

    [Header("Compute Shader")]
    [SerializeField] private ComputeShader computeShader;
    private int _computeShaderKernel;

    private ComputeBuffer _bufferPixelPositions; //Pixels positions used to send to the computer shader. Modified once
    private ComputeBuffer _bufferGravSources; //Gravitation sources used to send to the computer shader. Modified in each update
    private ComputeBuffer _bufferForcesInColor; //Color forces from the compute shader used. Modified in each update
    private Color[] _outputForcesInColor;

    private Texture2D _texture;
    private int _pixelCount;

    private float _maxForce;
    private SpaceObject[] _spaceObjects;
    private Source[] _gravitySources; // All objects with gravity. Store their position and mu (GravConstant*mass)

    private float _time;
    private float _waitSeconds = 0.01f;


    [Serializable]
    public struct Source
    {
        public Vector3 position;
        public float mu; //GravConstant*mass

        public Source(Vector3 position, float mu)
        {
            this.position = position;
            this.mu = mu;
        }
    }

    void Start()
    {
        _time = Time.realtimeSinceStartup;

        var spaceObjects = GameObject.FindGameObjectsWithTag("SpaceObject").Where(o => o.gameObject != gameObject).ToList();
        _spaceObjects = spaceObjects.Select(p => p.GetComponent<SpaceObject>()).ToArray();
        _maxForce = GetMaximumGravity();

        _texture = new Texture2D((int)_textureResolution.x, (int)_textureResolution.y)
        {
            wrapMode = TextureWrapMode.Clamp,
            filterMode = FilterMode.Bilinear
        };

        GetComponent<Renderer>().material.mainTexture = _texture;

        _gravitySources = GetSourcesData();

        InitializeComputeShaderForceMap();
    }

    void Update()
    {
        if (_time + _waitSeconds <= Time.realtimeSinceStartup)
        {
            UpdateComputeShaderForceMap();
            _time = Time.realtimeSinceStartup;
        }
        //UpdateComputeShaderForceMap();
    }

    void OnApplicationQuit()
    {
        _bufferPixelPositions?.Dispose();
        _bufferGravSources?.Dispose();
        _bufferForcesInColor?.Dispose();
    }

    private Source[] GetSourcesData()
    {
        var sources = new Source[_spaceObjects.Length];
        var gravitationalConstant = GameObject.Find("GameManager").GetComponent<GameManager>().GravitationalConstantUnityScaled;

        for (int i = 0; i < _spaceObjects.Length; i++)
        {
            sources[i].position = _spaceObjects[i].transform.position;
            sources[i].mu = (float)(_spaceObjects[i].Mass * gravitationalConstant);
        }

        return sources;
    }

    // This is important to initialize the variables in the compute shader.
    // Specially important to set the arrays size to be used in the compute shader.
    private void InitializeComputeShaderForceMap()
    {
        _pixelCount = _texture.height * _texture.width;

        _bufferPixelPositions = new ComputeBuffer(_pixelCount, sizeof(float) * 3);
        _bufferGravSources = new ComputeBuffer(_pixelCount, sizeof(float) * 4);
        _bufferForcesInColor = new ComputeBuffer(_pixelCount, sizeof(float) * 4);

        var texturePixelPositions = GetTextureWorldPoints();
        _bufferPixelPositions.SetData(texturePixelPositions);

        _computeShaderKernel = computeShader.FindKernel("CSForceMap");
        computeShader.SetBuffer(_computeShaderKernel, "gravSources", _bufferGravSources);
        computeShader.SetBuffer(_computeShaderKernel, "pixelPositions", _bufferPixelPositions);
        computeShader.SetBuffer(_computeShaderKernel, "forcesInColor", _bufferForcesInColor);

        computeShader.SetInt("numSources", _gravitySources.Length);
        computeShader.SetInt("sizeX", _texture.height);
        computeShader.SetInt("sizeY", _texture.width);
        computeShader.SetFloat("maxForce", _maxForce);

        _outputForcesInColor = new Color[_texture.height * _texture.width];
    }

    private Vector3[] GetTextureWorldPoints()
    {
        var worldPoints = new Vector3[_texture.height * _texture.width];

        for (int i = 0; i < _texture.height; i++)
        {
            for (int j = 0; j < _texture.width; j++)
            {
                var localPoint = TransformTextureCoordinateToLocalCoordinates(i, j, _texture);
                var worldPoint = transform.TransformPoint(localPoint);
                worldPoint.y = _positionTextureY; //We want to check with respect to reference planet (usually Earth) and not actual position of texture
                worldPoints[j * _texture.height + i] = worldPoint;
            }
        }

        return worldPoints;
    }

    // From i,j position in texture to a local Vector3
    private Vector3 TransformTextureCoordinateToLocalCoordinates(int i, int j, Texture2D texture)
    {
        var posX = 5 - 10 * (i + 0.5f) / texture.height;
        var posZ = 5 - 10 * (j + 0.5f) / texture.width;

        return new Vector3(posX, 0, posZ);
    }

    // Update Compute Shader variable: gravity sources.
    // Retrieve from Compute Shader: _bufferForcesInColor and sets them in _outputForcesInColor
    private void UpdateComputeShaderForceMap()
    {
        UpdateSourcesPosition();

        _bufferGravSources.SetData(_gravitySources);
        computeShader.Dispatch(_computeShaderKernel, _pixelCount / 32, 1, 1); //The dividing value should be the same as on the numthreads

        _bufferForcesInColor.GetData(_outputForcesInColor);

        _texture.SetPixels(_outputForcesInColor);
        _texture.Apply();
    }

    private void UpdateSourcesPosition()
    {
        for (int i = 0; i < _spaceObjects.Length; i++)
        {
            _gravitySources[i].position = _spaceObjects[i].transform.position; //No need to update the mu, it hasn't changed
        }
    }

    private float GetMaximumGravity()
    {
        var maxForce = float.MinValue;

        foreach (var spaceObject in _spaceObjects)
        {
            var force = GetGravity(spaceObject, spaceObject.transform.position + new Vector3(1.0f, 1.0f, 1.0f)).magnitude;

            if (maxForce <= force)
            {
                maxForce = force;
            }
        }

        return maxForce;
    }

    // Apply Log to the gravity to ease visualization of the force
    private Vector3 GetGravity(SpaceObject spaceObject, Vector3 atPoint)
    {
        var direction = spaceObject.transform.position - atPoint;
        var gravityLog = Math.Log(1 + spaceObject.GetGravitationalPullForce(direction.magnitude));

        return direction.normalized * (float)gravityLog;
    }
}


Optimization

The main function in the compute shader has this attribute [numthreads(x,y,z)] which I have very little knowledge of. The official documentation from Microsoft [4] and some Unity Answers [5] can give some information on the attribute, which is very hardware dependent.

It is worth noting that there is a maximum thread group count of 65535 (with a group of 32 the maximum texture size is 1448x1448, with a group of 64 the maximum texture size would be 2047x2047) that can be used. My code has a group of 32 and I will be using the texture of 1448x1448 in the comparisons.

Similar to the CPU case we can also add a timer to update the texture at specified moments. This improves performance slightly.

Fragment Shader

Compute shader allows calculations to be done in the GPU, and then you can retrieve the data to be used however you want. As we are trying to paint the values in a texture it made perfect sense to use a traditional shader for this task. Doing this would remove the intermediate step of sending the data to the C# script. The script will send the data back to the GPU where the texture is painted. 

As with the compute shader we have 2 components:
  • ForceMapShader.shader: This is a file that uses shader language and will be ran in the GPU. It does the calculations and paints in the texture.
  • ForceMapFragShader.cs: This script loads the information into the GPU.
To understand the full logic of the shader I recommend having some knowledge on this topic. Nevertheless, the logic used is pretty basic: I use the frag function to calculate the forces and paint them.

The major takeaways are:
  • Properties section: these are global variables that will be modified initially.
  • Frag function: Once shader initialization is complete do all the calculations and paint the texture.
  • Only update the minimum information required.
The logic is the same as with the compute shader but having the end result directly painting on the pixel. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
Shader "Gravity/ForceMap"
{
    Properties //I will use these as constants
    {
        _MainTex("Texture", 2D) = "white" {}
        _NumSources("Sources", int) = 0
        _SizeX("SizeX", int) = 0
        _SizeY("SizeY", int) = 0
        _MaxForce("MaxForce", float) = 0
    }
    SubShader
    {
        Tags { "RenderType" = "Opaque" }
        Pass
        {
            CGPROGRAM
            #pragma target 3.0
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                UNITY_FOG_COORDS(1)
                float4 vertex : SV_POSITION;
            };

            struct Source
            {
                float3 position;
                float mu;
            };

            Texture2D _MainTex;
            float4 _MainTex_ST;

            uint _NumSources;
            int _SizeX;
            int _SizeY;
            float _MaxForce;
            uniform StructuredBuffer<Source> gravSources; //This will get updated asyncrnously
            uniform StructuredBuffer<float3> pixelPositions;

            /*******/

            float4 GetColorFromGravity(float3 force)
            {
                float4 colorForce = float4(0, 0, 0, 0);

                if (force.z > 0.0f && force.x > 0.0f)
                {
                    colorForce.b = force.z;
                    colorForce.g = force.x;
                }
                else if (force.z > 0.0f && force.x <= 0.0f)
                {
                    colorForce.b = force.z;
                    colorForce.r = -force.x;
                }
                else if (force.z <= 0.0f && force.x > 0.0f)
                {
                    colorForce.r = -force.z;
                    colorForce.g = sqrt(pow(force.z, 2) + pow(force.x, 2));
                }
                else if (force.z <= 0.0f && force.x <= 0.0f)
                {
                    colorForce.r = sqrt(pow(force.z, 2) + pow(force.x, 2));
                    colorForce.g = -force.z;
                }

                return colorForce;
            }

            // Obtains the log of the gravity force vector
            float3 GetNormalizedForce(uint position)
            {
                float3 netForce = float3(0, 0, 0);

                for (uint k = 0; k < _NumSources; ++k)
                {
                    float3 forceDirection = (gravSources[k].position - pixelPositions[position]);
                    float gravityLog = log(1 + gravSources[k].mu / dot(forceDirection, forceDirection));
                    netForce += normalize(forceDirection) * gravityLog;
                }

                return netForce;
            }

            /*******/

            v2f vert(appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                UNITY_TRANSFER_FOG(o,o.vertex);
                return o;
            }

            fixed4 frag(v2f i) : SV_Target
            {
                fixed4 col;
                if (_NumSources == 0)
                {
                    col = float4(0, 0, 0, 0);
                }
                else
                {
                    int x = i.uv.x * _SizeX;
                    int y = i.uv.y * _SizeY;

                    float3 clampedForce = GetNormalizedForce(y*_SizeX + x) / _MaxForce;
                    col = GetColorFromGravity(clampedForce);
                }
                return col;
            }
            ENDCG
        }
    }
}


ForceMapFragShader.cs has a very similar logic to the compute shader:
  1. Initialization:
    1. Setup texture size and properties.
    2. Create world points for the texture.
    3. Initialize shader variables.
  2. Update shader variables:
    1. Send updated gravity sources to GPU.
    2. Shader doing magic: calculate pixel colors with the updated sources. Note that this is happening in parallel to this list.

Remarks

It is interesting that in this implementation the shader pixels are not smoothed out, but we can have almost any size we desired (maximum size 11585x11585).
 

Comparisons

For each approach I will only show the average FPS. I have access to the CPU main thread, CPU render thread and FPS, but for the sake of simplicity I will not show these other values. The data was taken from the Stats option in Unity and on Maximize On Play (screen resolution 1898x1068).

Testing rig: Intel i7 7700k 4.20 GHz, 16 GB RAM, Windows 10, Nvidia RTX 3070
Testing date: June-July 2021

Tests:
  • Test 1: Earth-Moon system (1 static, 1 dynamic object)
  • Test 2: Solar system (1 sun, 8 planets)
  • Test 3: Chaos (N Bodies)

Test 1: Earth-Moon system (1 static, 1 dynamic object)

This is a simple case of only 2 bodies in the scene.

2 Bodies. FPS values per texturing mode

Earth-Moon system displaying a force map. Fragment shader 5000x5000

Test 2: Solar system (1 sun, 8 planets)

The solar system visualization with all major planets. Dwarf planets (Ceres and Pluto) are not considered here.

9 Bodies. FPS values per texturing mode

Solar system. Outer worlds visible, inner worlds is the blue blob. Fragment  shader 5000x5000

Test 3: Chaos (36 Bodies)

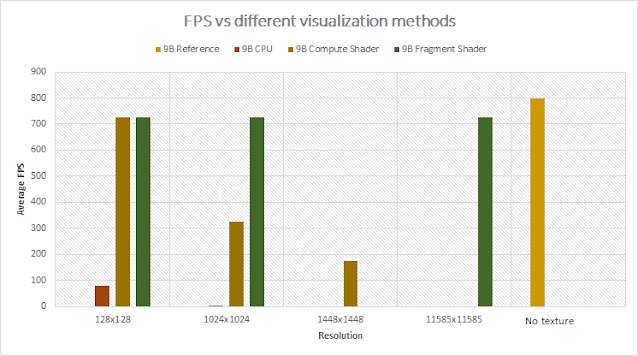
Modified Solar system to have a total of 36 bodies. 

36 Bodies. FPS values per texturing mode

Modified Solar system with 36 bodies. Fragment shader 3000x3000


The data shows that CPU is clearly a bottle neck. Among other methods Fragment is recommended, specially when it concerns increasing the resolution. It has great performance that barely decays with the resolution.

It is worth mentioning that there are factors that can affect the results:
  • To improve performance, we could add SystemDiagnostics and calculate the FPS in a stand-alone deployment. The unity editor generates some overhead.
  • Create a multi-threading implementation for the CPU approach.
Here I want to visually show the difference between each approach (CPU, Compute shader and Fragment shader).

The gravitation system has repetitive calculations in the FixedUpdate per object, which in return affect the general FPS. This is easily seen in the Chaos example.

Note: for the tests I had to disable the trail as it was creating a decent overhead in the results, though the GIFs shown here will display the trail.
 

Conclusion

For any type of heavy math operations independent of each other it is highly recommended to use the GPU. The speed at which it processes the data cannot be compared to anything else. It is true the CPU solution does not use multiple threads (which could improve the results considerably), but I doubt it can reach the Fragment Shader’s FPS.

This is just a quick post showing how to implement the math using 3 different approaches, and they could be improved. I am not interested in doing a foolproof analysis here, but an initial estimation.

As with the previous post a sample project can be found on this download link with all the relevant code.
Unity version: 2020.2.7f1

Hopefully this can bring my readers some insights.

References

[1] Unity Documentation Texture2D, Version 2020.3, Accessed 21 June 2021, <https://docs.unity3d.com/ScriptReference/Texture2D.html>

[2] Unity Documentation Compute shader, Version 2020.3, Accessed 21 June 2021, <https://docs.unity3d.com/Manual/class-ComputeShader.html>

[3] Ronja’s Tutorials Compute Shader, July 26 2020, Accessed 21 June 2021, <https://www.ronja-tutorials.com/post/050-compute-shader/>

[4] Microsoft Documentation, 2021, Accessed 21 June 2021, <https://docs.microsoft.com/en-us/windows/win32/direct3dhlsl/sm5-attributes-numthreads>

[5] Unity Answers, Difference Between Calling numthreads and Dispatch in a Unity Compute Shader, July 25th 2020, Accessed 21 June 2021, <https://stackoverflow.com/questions/63034523/difference-between-calling-numthreads-and-dispatch-in-a-unity-compute-shader>

[6] Nvidia Developer Zone, Cg 3.1 Toolkit Documentation, Accessed 24 June 2021, <https://developer.download.nvidia.com/cg/index_stdlib.html>
By at No comments:
Labels: , , , , ,
Location: Badalona, Barcelona, Spain

Wednesday, June 16, 2021

Gravity Part 2: Orbit Predictions (One-Body problem)

Introduction

This is the second post in the series I am creating, based on the logic from Physics-based Solar System Lessons:
The previous post sets the foundations in which part 2 and 3 are built upon. Part 1 was mandatory as there have been many changes since the original Physics-based Solar System Lessons post.

Gravity Part 2: Orbit Predictions (One-Body problem)

Once we have a system affected only by gravitational forces, the next logical step was to predict orbits of objects. This is not a trivial task, especially when there are multiple bodies in play. I focused on implementing object trajectory predictions for One-Body problems.

Orbital mechanics sketch (image credit: wikipedia [4])


Background

All the math and concepts behind the One/N-Body problems have been obtained from the books by Keeton, C. (2014) [1] and Walter, U. (2018) [2].

What is a One-Body problem? 
A system in which the source of gravity is stationary while another object is in motion (and therefore affected by the stationary object’s gravity).
 
What is a Two-Body Problem?
A system in which two objects interact with each other through their force of gravity.

Can we predict orbits?

There are 3 different problems to predicting trajectories:
  • One-Body problem: Solving the prediction is not complicated. The visual representation is simple as the trajectory will be fixed in time.
  • Two-Body problem: Things become tricky as both objects move in time. Any visualization would be complicated as the forces applied will change as objects move in time.
  • N-Body problem: This is a generalization of the Two-body problem to a larger scale. As mentioned before, visualization of the orbits would be complicated.
There are two possibilities to visualize the trajectories:
  • Given a system, let it run for a certain amount of time and we can visualize the position and velocity of the objects. This can be used to predict N-Body problems and see the future trajectories, but it will not give you any past trajectories.
  • Given a function obtain the past and future trajectory of an object. This is simple and doable for a One-Body problem.
Disclaimer: There are ways to solve N-Body problems numerically, but I have not tried to apply the math in Unity.

The first option can be used by setting up a system with the information provided in Gravity Part 1: An update. The second option is what I am going to explain in this post.

Predictions

As we are focused on One-Body problems, we will always have one of these trajectories:
  • Elliptical/Circular: object “captured” by the gravity of the massive object.
  • Parabolic: Object that is passing just fast enough to escape gravitation pull.
  • Hyperbolic: Object that is passing too fast and escapes gravitation pull.
Calculations for elliptical trajectories are easy, but those for parabolic and hyperbolic are a bit more complex. All these trajectories come from conic sections. The parabolic trajectory is a fringe case that I will not implement, but it can be added following the same logic as it is for elliptic/hyperbolic.

To create these conics I will be using the following data:
  • A Massive object that is the primary force attraction:
    • Given its position.
    • Given its gravity force.
  • Another object that we want to check its trajectory:
    • Given its position.
    • Given its velocity and direction.

The Code

From this point onwards I will be explaining the math as well as the code I have used. The code can be summarized into 2 parts:
  • Conics: Conic shape trajectories.
  • Orbit: Calculation of the trajectory using conic shapes.

Conics

As can be observed by the following picture the conic family can create the desired trajectories: Circular, Elliptical, parabolic, and hyperbolic.

Conic sections and orbits (image credit: braeunig [3])

All conics have the same basic structure, as such I created an interface IConic that affects all.
    
    
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

using System.Collections.Generic;
using System.Collections.ObjectModel;
using UnityEngine;

interface IConicSection
{
    double SemiMajorAxis { get; }
    double SemiMinorAxis { get; }
    double Eccentricity { get; }
    double Distance { get; }
    ReadOnlyCollection<Vector3> Points { get; }

    List<Vector3> GetPointsInWorldCoordinates(Transform objectTransform);
    void SetConicSectionTransform(Transform orbitPlane, Vector3 focusPoint, Vector3 pointInTrajectory, bool isVelocityIncreasing);
}


It is worth mentioning that both ellipse and hyperbola will get all equation variables in the constructor from the eccentricity and semi major axis. Here is an explanation of the public functions:

GetPointsInWorldCoordinates(...): 
Given a transform (rotation and traslation) obtain the trajectory points in world coordinates

SetConicSectionTransform(...):
Modify the Orbit Object transform component to be aligned with the conic section. We need to know whether the velocity is increasing to obtain the correct angle of the object in the conic segment.

Ellipse trajectory

This also considers the Circular trajectory as it is a fringe case of the ellipse. We need to solve the basic (no translation nor rotation) ellipse equation:

\[ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\]
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
using System;
using System.Collections.Generic;
using System.Collections.ObjectModel;
using System.Linq;
using UnityEngine;

public class Ellipse : IConicSection
{
    #region Properties
    public double SemiMajorAxis { get; private set; }
    public double SemiMinorAxis { get; private set; }
    public double Eccentricity { get; private set; }
    public double Distance { get; private set; } //Foci Distance
    public ReadOnlyCollection<Vector3> Points { get; private set; }
    #endregion

    #region Public Methods
    /// <summary>
    /// Basic ellipse in Unity default units, centered in the origin and no rotation applied
    ///   x^2/a^2 + y^2/b^2 = 1
    /// 
    ///   a = SemiMajorAxis
    ///   b = SemiMinorAxis
    /// </summary>
    /// <param name="eccentricity"> Ellipse eccentricity [0,1] </param>
    /// <param name="semiMajorAxis"> Length of the semi major axis </param>
    public Ellipse(double eccentricity, double semiMajorAxis, int numberOfPoints = 10)
    {
        Eccentricity = eccentricity;
        SemiMajorAxis = semiMajorAxis;
        SemiMinorAxis = CalculateSemiMinorAxis();
        Distance = CalculateFociDistance();

        CreateEllipseLocalPoints(numberOfPoints);
    }

    /// <summary>
    /// Get all the local points in world coordinates, applying:
    ///  - A specific transform (position, normal and rotation around local Y)
    /// </summary>
    /// <param name="objectTransform"> An object's transform </param>
    /// <returns> Ellipse points in world coordinates </returns>
    public List<Vector3> GetPointsInWorldCoordinates(Transform objectTransform)
    {
        return Points.Select(p => objectTransform.TransformPoint(p)).ToList();
    }

    /// <summary>
    /// Given the orbit plane, an ellipse focus point, an object's position in the 
    /// ellipse (and if it is accelerating), adjust the orbit plane position and its 
    /// rotation so a projection of the ellipse is correct in world coordinates.
    /// </summary>
    /// <param name="orbitPlane"> where the Ellipse will be projected </param>
    /// <param name="focusPoint"> ellipse focus </param>
    /// <param name="pointInTrajectory"> point in the ellipse edge </param>
    /// <param name="isVelocityIncreasing"> is point in trajectory increasing speed? used to get the correct angle </param>
    public void SetConicSectionTransform(Transform orbitPlane, Vector3 focusPoint, Vector3 pointInTrajectory, bool isVelocityIncreasing)
    {
        //Set position
        var distanceFromObject = Vector3.Distance(pointInTrajectory, focusPoint);
        var angleRadians = GetAngleBetweenPointInEllipseAndSemiMajorAxis(distanceFromObject, isVelocityIncreasing);

        var rot = Quaternion.AngleAxis(-(float)angleRadians * Mathf.Rad2Deg, orbitPlane.up);
        var semiMajorAxisDirection = (rot * (focusPoint - pointInTrajectory)).normalized;
        orbitPlane.position = focusPoint + semiMajorAxisDirection * (float)Distance;

        //Set rotation
        var semiMajorAxisDirectionLocal = orbitPlane.InverseTransformDirection(semiMajorAxisDirection);
        var angle = Vector3.Angle(semiMajorAxisDirectionLocal, Vector3.right);

        orbitPlane.Rotate(Vector3.up, angle, Space.Self);
        var localPos = orbitPlane.InverseTransformPoint(pointInTrajectory);

        if (!IsPointInEdge(localPos))
        {
            orbitPlane.Rotate(Vector3.up, -angle * 2, Space.Self);
        }
    }
    #endregion


    #region Private Methods
    private double CalculateSemiMinorAxis()
    {
        return SemiMajorAxis * Math.Sqrt(1 - Math.Pow(Eccentricity, 2));
    }

    private double CalculateFociDistance()
    {
        return Math.Sqrt(Math.Pow(SemiMajorAxis, 2) - Math.Pow(SemiMinorAxis, 2));
    }

    private void CreateEllipseLocalPoints(int numberOfPoints)
    {
        var points = new List<Vector3>();
        var gap = 360.0f / numberOfPoints;

        for (int i = 0; i < numberOfPoints; i++)
        {
            var theta = (i * gap) * Mathf.Deg2Rad;
            var x = SemiMajorAxis * Mathf.Cos(theta);
            var z = SemiMinorAxis * Mathf.Sin(theta);

            points.Add(new Vector3((float)x, 0, (float)z));
        }

        points.Add(points[0]);
        Points = points.AsReadOnly();
    }

    //Get the angle using the orbit equation
    private double GetAngleBetweenPointInEllipseAndSemiMajorAxis(double distance, bool isIncreasingVelocity)
    {
        var cosE = GetCenterCosAngleFromOrbitEquation(distance);
        var angle = Math.Acos((cosE - Eccentricity) / (1 - Eccentricity * cosE));

        return isIncreasingVelocity ? angle : -angle;
    }

    private double GetCenterCosAngleFromOrbitEquation(double distance)
    {
        return -(distance / SemiMajorAxis - 1) / Eccentricity;
    }

    /// <summary>
    /// Verify if the given point is in the ellipse
    /// </summary>
    /// <param name="point"> a point in 3D, note the Y-axis is not used here </param>
    /// <returns></returns>
    private bool IsPointInEdge(Vector3 point)
    {
        return Math.Abs(Math.Pow(point.x, 2) / Math.Pow(SemiMajorAxis, 2) + Math.Pow(point.z, 2) / Math.Pow(SemiMinorAxis, 2) - 1) < Constants.EPSILON;
    }
    #endregion
}

Note: to obtain the rotation with respect to the focus we use the orbit equation and its derivation. To follow the math I followed the formulas provided by Walter (equations 7:4:14) [2]
 

Hyperbolic trajectory:

We need to solve the basic (no translation nor rotation) hyperbolic equation:

\[ \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1\]
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
using System;
using System.Collections.Generic;
using System.Collections.ObjectModel;
using System.Linq;
using UnityEngine;

public class Hyperbola : IConicSection
{
    #region Properties
    public double SemiMajorAxis { get; private set; }
    public double SemiMinorAxis { get; private set; }
    public double Eccentricity { get; private set; }
    public double Distance { get; private set; } //Minimum distance from foci to edge
    public double SemiLatusRectum { get; private set; }
    public ReadOnlyCollection<Vector3> Points { get; private set; }
    #endregion

    #region Public Methods
    /// <summary>
    /// Basic hyperbola in Unity default units, centered in the origin and no rotation applied
    ///   x^2/a^2 - y^2/b^2 = 1
    /// 
    ///   a = SemiMajorAxis
    ///   b = SemiMinorAxis
    /// </summary>
    /// <param name="eccentricity"> Hyperbola eccentricity > 1 </param>
    /// <param name="semiMajorAxis"> Length of the semi major axis </param>
    public Hyperbola(double eccentricity, double semiMajorAxis, int numberOfPoints = 10)
    {
        Eccentricity = eccentricity;
        SemiMajorAxis = semiMajorAxis;
        SemiMinorAxis = CalculateSemiMinorAxis();
        Distance = CalculateMinimumDistance();
        SemiLatusRectum = SemiMajorAxis * (1 - Math.Pow(Eccentricity, 2));        

        CreateHyperbolaLocalPoints(numberOfPoints);
    }

    /// <summary>
    /// Get all the local points in world coordinates, applying:
    ///  - A specific transform (position, normal and rotation around local Y)
    /// </summary>
    /// <param name="objectTransform"> An object's transform </param>
    /// <returns> Hyperbola points in world coordinates </returns>
    public List<Vector3> GetPointsInWorldCoordinates(Transform objectTransform)
    {
        return Points.Select(p => objectTransform.TransformPoint(p)).ToList();
    }

    /// <summary>
    /// Given the orbit plane, a hyperbola focus point, an object's position in the 
    /// hyperbola (and if it is accelerating), adjust the orbit plane position and its 
    /// rotation so a projection of the hyperbola is correct in world coordinates.
    /// </summary>
    /// <param name="orbitPlane"> where the Hyperbola will be projected </param>
    /// <param name="focusPoint"> hyperbola focus </param>
    /// <param name="pointInTrajectory"> point in the hyperbola edge </param>
    /// <param name="isVelocityIncreasing"> is point in trajectory increasing speed? </param>
    public void SetConicSectionTransform(Transform orbitPlane, Vector3 focusPoint, Vector3 pointInTrajectory, bool isVelocityIncreasing)
    {
        //Set position
        orbitPlane.position = focusPoint;

        //Set rotation
        float angle = GetAngle(orbitPlane, focusPoint, pointInTrajectory, isVelocityIncreasing);

        orbitPlane.Rotate(Vector3.up, angle, Space.Self);        
        var localPos = orbitPlane.InverseTransformPoint(pointInTrajectory);

        if (!IsPointInEdge(localPos))
        {
            orbitPlane.Rotate(Vector3.up, -angle * 2, Space.Self);
        }
    }
    #endregion


    #region Private Methods
    private double CalculateSemiMinorAxis()
    {
        return -SemiMajorAxis * Math.Sqrt(Math.Pow(Eccentricity, 2) - 1);
    }

    private double CalculateMinimumDistance()
    {
        return SemiMajorAxis * (1 - Eccentricity);
    }

    private void CreateHyperbolaLocalPoints(int numberOfPoints)
    {
        var pointsPositive = new List<Vector3>();
        var pointsNegative = new List<Vector3>();
        var offset = -SemiMajorAxis + Distance;

        for (int i = 0; i < numberOfPoints / 2; ++i)
        {
            var z = i * i / 5;
            var x = (float)(SemiMajorAxis * Math.Sqrt(1 + Math.Pow(z, 2) / Math.Pow(SemiMinorAxis, 2)) + offset);

            pointsPositive.Add(new Vector3(x, 0, z));

            if (i != 0)
            {
                pointsNegative.Add(new Vector3(x, 0, -z));
            }

        }

        pointsPositive.Reverse();
        pointsPositive.AddRange(pointsNegative);
        Points = pointsPositive.AsReadOnly();
    }

    private float GetAngle(Transform orbitPlane, Vector3 focusPoint, Vector3 pointInTrajectory, bool isVelocityIncreasing)
    {
        var distanceFromObject = Vector3.Distance(focusPoint, pointInTrajectory);
        var angleRadians = Math.Acos((SemiLatusRectum / distanceFromObject - 1) / Eccentricity);

        angleRadians = (isVelocityIncreasing) ? -angleRadians : angleRadians;

        var rot = Quaternion.AngleAxis((float)angleRadians * Mathf.Rad2Deg, orbitPlane.up);

        var semiMajorAxisDirection = (rot * (pointInTrajectory - focusPoint)).normalized;
        var semiMajorAxisDirectionLocal = orbitPlane.InverseTransformDirection(semiMajorAxisDirection);
        var angleLocal = Vector3.Angle(semiMajorAxisDirectionLocal, Vector3.right);

        return angleLocal;
    }

    /// <summary>
    /// Verify if the given point is in the hyperbola. Offset applied as the points are not
    /// centered in the "center" of the hyperbola, but 1 of the focus points.
    /// </summary>
    /// <param name="point"> a point in 3D, not the Y-axis is not used here </param>
    /// <returns></returns>
    private bool IsPointInEdge(Vector3 point)
    {
        var offset = new Vector3((float)(Distance - SemiMajorAxis), 0, 0);
        point -= offset;

        var distanceToEdge = Math.Abs(Math.Pow(point.x, 2) / Math.Pow(SemiMajorAxis, 2) - Math.Pow(point.z, 2) / Math.Pow(SemiMinorAxis, 2) - 1);
        return distanceToEdge < Constants.EPSILON;
    }
    #endregion
}

Note: The function GetAngle(...) returns the angle from Vector3.Angle which outputs a value [0, 180]. As it is missing the [180, 360] range we check if the object is in the trajectory.

Orbit

The Orbit code basically consists of the functionality that will trigger the orbit creation and visualization. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
using System;
using UnityEngine;
using static Constants;

public class Orbit : MonoBehaviour
{
    public GameObject OrbitingObject { get; private set; }
    public GameObject OrbitAroundObject { get; private set; }
    public OrbitTrajectory OrbitTrajectory { get; private set; } = OrbitTrajectory.Undefined;

    private GameManager _gameManager;
    private LineRenderer _lineRenderer;
    private IConicSection _conicSection;

    public void CreateOrbit(GameObject orbitAroundObject, GameObject orbitingObject)
    {
        _gameManager = GameObject.Find("GameManager").GetComponent<GameManager>();

        OrbitingObject = orbitingObject;
        OrbitAroundObject = orbitAroundObject;

        var isVelocityIncreasing = OrbitingObject.GetComponent<SpaceObject>().IsVelocityIncreasing;

        _conicSection = CreateConicSection();
        _conicSection.SetConicSectionTransform(transform, OrbitAroundObject.transform.position, OrbitingObject.transform.position, isVelocityIncreasing);
        var realWorlTrajectoryPoints = _conicSection.GetPointsInWorldCoordinates(transform);

        _lineRenderer = GetComponent<LineRenderer>();
        _lineRenderer.positionCount = realWorlTrajectoryPoints.Count;
        _lineRenderer.SetPositions(realWorlTrajectoryPoints.ToArray());
    }

    private IConicSection CreateConicSection()
    {
        var focusPoint = OrbitAroundObject.transform.position;
        var point = OrbitingObject.transform.position;
        var distance = Vector3.Distance(point, focusPoint);

        var velocity = OrbitingObject.GetComponent<Rigidbody>().velocity;
        var mu = _gameManager.GravitationalConstantUnityScaled * OrbitAroundObject.GetComponent<SpaceObject>().Mass;

        var semiMajorAxis = Math.Pow(2 / (double)distance - Math.Pow(velocity.magnitude, 2) / mu, -1);
        var orbitNormal = -Vector3.Cross(velocity, focusPoint - point);

        transform.up = orbitNormal.normalized;

        var angularMomentum = orbitNormal.magnitude;
        var semiLatusRectum = Math.Pow(angularMomentum, 2) / mu;
        var eccentricity = Math.Sqrt(1 - semiLatusRectum / semiMajorAxis);
        
        IConicSection conicSection;

        if (IsObjectInEllipticalOrbit())
        {
            conicSection = new Ellipse(eccentricity, semiMajorAxis, 50);
            OrbitTrajectory = OrbitTrajectory.Elliptical;
        }
        else
        {
            conicSection = new Hyperbola(eccentricity, semiMajorAxis, 50);
            OrbitTrajectory = OrbitTrajectory.Escape;
        }

        return conicSection;
    }

    private bool IsObjectInEllipticalOrbit()
    {
        var ellipsePointVelocity = OrbitingObject.GetComponent<Rigidbody>().velocity;
        var distance = (OrbitAroundObject.transform.position - OrbitingObject.transform.position).magnitude;
        var escapeVelocity = OrbitAroundObject.GetComponent<SpaceObject>().GetEscapeVelocity(distance);

        return ellipsePointVelocity.magnitude < escapeVelocity;
    }
}

It is worth mentioning that all the conics need the eccentricity and semimajor axis to be calculated. These are obtained through simple formulas:

Semi major axis:
\[ a = \frac{1}{\sqrt{\frac{2}{d} -  \frac{v^{2}}{\mu} }}\]
\[ \mu  = G m\]
where d is the distance between objects, v is the velocity of the orbiting object, G is the gravitational constant and m is the mass of the gravity source.

Eccentricity:
\[ e  = \sqrt{1 - \frac{L}{a}}\]
\[ L  = \frac{p^{2}}{\mu}\]
where L is the Semi latus Rectum and p is the angular momentum.

One last thing worth mentioning is how I obtain the orbit normal vector. The code is a simplification of the actual operation. For better visibility I will put here the logic used:

1
2
3
4
Vector3 pointA = point + velocity;
Vector3 pointB = focusPoint;
Vector3 orbitNormal = Vector3.Cross(pointA - point, pointB - point);
//Vector3 orbitNormal = Vector3.Cross(-velocity, focusPoint - point);

Updates

After creating the orbit predictions, some changes were made to the Constants.cs and SpaceObject.cs files. 
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public static class Constants
{
    public static readonly double GRAVITATIONAL_CONSTANT_KM = 6.67430e-20; //N*km^2/kg^2
    public static readonly double EPSILON = 0.01;

    public const int FREE_VELOCITY = 0;
    public const int CIRCULAR_ORBIT_VELOCITY = 1;
    public const int ESCAPE_ORBIT_VELOCITY = 2;

    public const int UNDEFINED = -1;
    public const int COLLISION = 0;
    public const int ELLIPTICAL = 1;
    public const int ESCAPE = 2;    

    public enum InitialVelocity
    {
        Free = FREE_VELOCITY,
        CircularOrbit = CIRCULAR_ORBIT_VELOCITY,
        EscapeOrbit = ESCAPE_ORBIT_VELOCITY
    }

    public enum OrbitTrajectory
    {
        Undefined = UNDEFINED,
        Collision = COLLISION,
        Elliptical = ELLIPTICAL,
        Escape = ESCAPE
    }
}

In the constants I just created some variables to keep track of the state, though there is no functionality attached to it.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
using System;
using System.Linq;
using UnityEngine;
using static Constants;

public class SpaceObject : Gravity
{
    #region variables
    [Header("Orbit related")]
    [SerializeField] private GameObject _orbit;

    [Header("Velocity settings")]
    [SerializeField] private Vector3 _initialDirection = new Vector3(0, 0, 1);
    [SerializeField] private InitialVelocity _velocityType = InitialVelocity.Free;
    [SerializeField] private double _initialVelocity = 0; // In standard km/s
    
    [Header("SpaceObject Properties")]

    [SerializeField]
    [Tooltip("external gravity forces do not affect this object")]
    private bool _disableGravityAffected = false;

    [SerializeField]
    [Tooltip("Kilograms")]
    private double _mass = 0; //Kg

    [SerializeField]
    [Tooltip("Kilometers")]
    private double _radius = 0; //km

    [SerializeField]
    [Tooltip("Kilometers. Distance at which entry to atmosphere happens")]
    private double _entryInterfaceDistance = 0; //Km. distance at which entry to atmosphere happens

    private Rigidbody _rigidbody;
    private GameObject _orbitAround;
    private bool initializationComplete = false;

    [Header("Debug")]
    [SerializeField] private double _currentVelocity = 0; // In standard km/s
    #endregion

    #region Properties
    public double Mass => _mass;

    public double CollisionDistance { get => (_radius + _entryInterfaceDistance) / _gameManager.SpaceScaleKm; }

    public double CurrentVelocity
    {
        get { return _currentVelocity * _gameManager.TimeScale / _gameManager.SpaceScaleKm; }
        set { _currentVelocity = value * _gameManager.SpaceScaleKm / _gameManager.TimeScale; }
    }

    public bool IsVelocityIncreasing { get; private set; } = true;
    #endregion

    void Awake()
    {
        var spaceObjects = GameObject.FindGameObjectsWithTag("SpaceObject").Where(o => o.gameObject != gameObject).ToArray();
        _rigidbody = GetComponent<Rigidbody>();

        InitializeGravity(spaceObjects, _mass);
    }

    void Update()
    {
        //This code would go on a game controller and affect desired objects.
        if (Input.GetKeyDown(KeyCode.Space))
        {
            if (!_disableGravityAffected)
            {
                SetOrbit();
            }
        }
    }

    void FixedUpdate()
    {
        try
        {
            if (!initializationComplete)
            {
                Initialization();
            }

            if (!_disableGravityAffected)
            {
                _rigidbody.velocity += GetExternalNetGravityVector();
            }

            UpdateVelocityStatus();
        }
        catch (Exception e)
        {
            throw new SystemException("Problem obtaining gravity: " + e);
        }
    }

    private void UpdateVelocityStatus()
    {
        if (CurrentVelocity != _rigidbody.velocity.magnitude)
        {
            IsVelocityIncreasing = (CurrentVelocity < _rigidbody.velocity.magnitude) ? true : false;
        }

        CurrentVelocity = _rigidbody.velocity.magnitude;
    }

    private void Initialization()
    {
        _initialVelocity = GetInitialVelocity(_velocityType);
        _rigidbody.velocity = _initialDirection.normalized * (float)_initialVelocity;

        _initialVelocity = _initialVelocity * _gameManager.SpaceScaleKm / _gameManager.TimeScale;

        initializationComplete = true;
    }


    private double GetInitialVelocity(InitialVelocity initialVelocityType)
    {
        if (_spaceObjects.Length == 0)
        {
            throw new SystemException("No SpaceObjects found. Need at least 1 to get velocity");
        }

        _orbitAround = _spaceObjects
          .OrderByDescending(o => o.GetComponent<SpaceObject>().GetGravitationalPullForce(
          (o.transform.position - transform.position).magnitude))
          .First();

        var distance = (_orbitAround.transform.position - transform.position).magnitude;
        var velocity = 0.0;

        switch (initialVelocityType)
        {
            case InitialVelocity.CircularOrbit:
                velocity = _orbitAround.GetComponent<SpaceObject>().GetVelocityForCircularOrbit(distance) + _orbitAround.GetComponent<Rigidbody>().velocity.magnitude;
                break;
            case InitialVelocity.EscapeOrbit:
                velocity = _orbitAround.GetComponent<SpaceObject>().GetEscapeVelocity(distance);
                break;
            default: //Free velocity                
                velocity = _initialVelocity * _gameManager.TimeScale / _gameManager.SpaceScaleKm;
                break;
        }

        return velocity;
    }

    private void SetOrbit()
    {
        var target = _spaceObjects.First().GetComponent<SpaceObject>();
        target.GetOrbitFromCurrentVelocity(gameObject, ref _orbit);
    }
}

The code added here only affects the user input to create the orbit. This could easily be in some type of game controller that only affects the desired objects. How this is triggered would be completely project-depended. I decided to keep it here for the sake of simplicity, though it should be somewhere else. As this is global to every object with an Orbit, triggering it will display the orbits of every single object.

Unity setup

The setup to have the orbit working is very simple. We need a child Orbit GameObject to the orbiting object
Add Orbit to SpaceObject script

The orbit object just needs 2 components: A line renderer and the Orbit script:

Components required for the Orbit GameObject


Now that the setup is finished let's view a few GIFs with elliptical and hyperbolic trajectory predictions. The blue line is the object's trail. The brown line is the predicted trajectory.

Circular trajectory prediction

Elliptic trajectory prediction

Hyperbolic trajectory prediction

All these examples are in the XZ plane, to keep it simple, but they work in any other plane.

Conclusions

This is an upgrade from the previous blog entry to add One-Body problem solutions for any single object. The implementation for N-Body problems is more complicated and maybe one day I will look into it. 

As with the previous post a sample project can be found on this download link with all the relevant code.
Unity version: 2020.2.7f1

The next post will look into painting a force map using CPU, Computational and Vertex shader.

References  

[1] Keeton, C. (2014). Principles of Astrophysics Using Gravity and Stellar Physics to Explore the Cosmos. https://doi.org/10.1007/978-1-4614-9236-8

[2] Walter, U. (2018). Astronautics The Physics of Space Flight. https://doi.org/10.1007/978-3-319-74373-8

Images:

[3] Robert A. Braeunig, Figure 4.1, digital image, accessed 16 June 2021, < http://www.braeunig.us/space/orbmech.htm>

[4] Angular Parameters of Elliptical Orbit, 2005, digital image, accessed 15 June 2021, < https://en.wikipedia.org/wiki/N-body_problem#/media/File:Angular_Parameters_of_Elliptical_Orbit.png>
By at No comments:
Labels: , , , ,
Location: Badalona, Barcelona, Spain
Subscribe to: Posts (Atom)

Gravity Part 3: Create a force map and display it (CPU, Compute Shader and Fragment Shader)

Introduction This is the third and last post in the series I am creating, based on the logic from Physics-based Solar System Lessons : ...